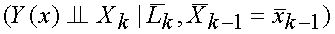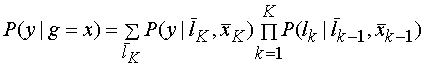Question to author:
The following paragraph appears on p. 103, shortly after eq. 3.63 in my copy of Causality:

"To place this result in the context of our analysis in this chapter, we note that the class of semi-Markovian models satisfying assumption (3.62) corresponds to complete DAGs in which all arrowheads pointing to X_k originate from observed variables."

It looks to me like this is a sufficient, but not necessary, condition to satisfy 3.62. It appears to me that the necessary condition is that no confounder exist between any X_i and L_j with i < j and that no confounder exist between any X_i and the outcome variable Y. However, a confounding arc between any X_i and X_j, or a confounding arc between L_i and X_j with i <= j, should not render the causal effect non-identifiable. For example, even if a confounding arc exists between X₂ and X₃ (but no other confounding arcs exist in the model), the causal effect on Y of setting X₂=x₂ and X₃=x₃ should be the same as the distribution on Y if we observe x₂ and x₃.

It is also not necessary that the DAG be complete.

Author reply:
You are right that the DAG need not be complete, and that the condition cited in p. 103 is sufficient but not necessary for either
(3.62)
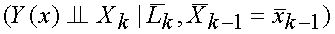
or the G-estimation formula
(3.63)
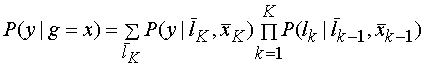
to hold. Corrections to the wordings of page 103 were posted on this website.

Your suggestion to allow confounding arcs beween X_i and X_j, is valid. However, allowing a confounding arc between L_i and X_j (with i < j) is too permissive, as can be seen by the non-identified models of Figure 3.9 (b), (c), (d) and (g) in Causality.

In general, condition (3.62) is both over-restrictive and lacks intuitive basis. A more general and intuitive condition leading to (3.63) is formulated in (4.5) (Causality, p 122), which reads as follows:

(3.62*) General condition for g-estimation
P(y|g = x) is identifiable and is given by (3.63) if every action-avoiding back-door path from X_k to Y is blocked by some subset L_k of non-descendants of X_k. (By "action-avoiding" we mean a path containing no arrows entering an X variable later than X_k.)

Comment 1: The new definition leads to improvements over (3,62), namely, there are cases where the g-formula (3.63) is valid with a subset L_k of the past but not with the entire past.
Example 1:

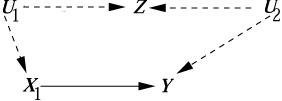
Assuming U₁ and U₂ are unobserved, and temporal order: U₁,Z, X₁, U₂,Y we see that (3.62*), hence (3.63), are satisfied with L₁ = 0, while taking the whole past L₁ = Z would violate both.

(3.62) is also satisfied with the choice L₁=0, but not with L₁=Z.

Comment 2: Defining L_k as the set of "nondescendants" of X_k (as opposed to temporal predecessors of X_k) also broadens (3.62).

Example 2:

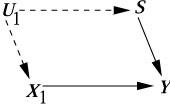
with temporal order: U₁,X₁, S,Y

Both (3.62) and (3.62*) are satisfied with L₁ = S, but not with L₁ = 0.

Comment 3: There are cases where (3.62) will not be satisfied even with the new interpretation of L_k, but the graphical condition (3.62*) is.

Example 3: (constructed by Ilya Shpitser)

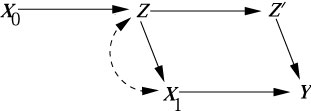
It is easy to see that (3.62*) is satisfied; all back-door action-avoiding paths from X₁ to Y are blocked by X₀, Z, Z'.

At the same time, it is possible to show, though by a rather intricate method (see the Twin Network Method, page 213) that Y{x₁, x₂} is not independent of X1, given Z, Z' and X₀.

(In the twin network model there is a d-connected path from X₁ to Y_x, as follows: X₁ <--> Z <--> Z* --> Z'* --> Y*) Therefore, (3.62) is not satisfied for Y{x₁,x₂} and X₁.)

This example demonstrates one weakness of the Potential Response approach initially taken by Robins in deriving (3.63). The counterfactual condition (3.62) that legitimizes the use of the g-estimation formula is void of intuitive support, hence, epidemiologists who apply this formula are doing so under no guidance of substantive medical knowledge. Fortunately, graphical methods are slowly making their way into epidemiological practice, and more and more people begin to understand the assumptions behind g-estimation.

(Warning: Those who currently reign causal analysis in statistics are incurably graph-o-phobic and ruthlessly resist attempts to enlighten their students, readers and co-workers with graphical methods. This slows down progress in statistical research, but will eventually be overrun by commonsense.)

Next discussion (CS262Z: Identifying conditional plans

Return to Discussions