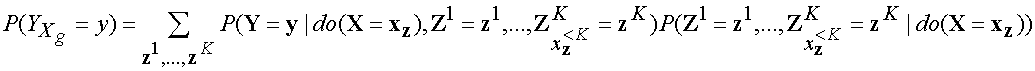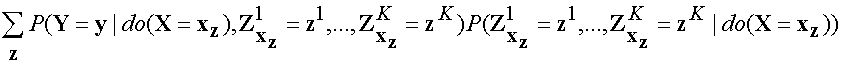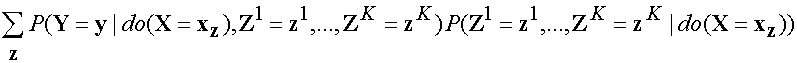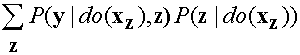CAUSALITY - Discussion (CS262Z)
Date: May 8, 2006
From: UCLA Students in CS262Z (Seminar in Causality, Spring, 2006)
Subject: Identifying conditional plans
Question to author:
Section 4.2 of the book (p. 113)
gives an identification condition and estimation
formula for the effect of a conditional action,
namely, the effect of an action do(X=g(z)) where
Z is a measurement taken prior to the action.
Is this equation generalizable to the case of
several actions, i.e., conditional plan?
The difficulty seen is that this formula
was derived on the assumption that
X does not change the value of Z. However, in
a multi-action plan, some actions in X could
change observations Z that are used
to guide future actions.
We do not have notation for distinguishing
post-intevention from pre-intevention observations.
Author reply (with Ilya Shpitser)
The need for notational distinction between
post-intevention from pre-inter-vention observations
is valid, and will be satisfied in Chapter 7 where we deal
with counterfactuals. The case of conditional
plans, however, can be handled without resorting to richer
notation. The reason is that the observations which dictate
the choice of an action are not changed by that action,
while those that have changed by previous actions are
well captured by the P(y|do(x),z) notation.
To see that this is the case, however, we will need to
introduce counterfactual notation, and then show how
it can be eliminated from our expression. We will use
bold letters to denote sets, and normal letters to denote
individual elements. Also, capital letters will denote
random variables, and small letters will denote possible
values these variables could attain.
We will write Yx to mean 'the value Y attains
if we set variables X to values x.'
Similarly, YXg is taken to mean
'the value Y attains if we set variables X to
whatever values they would have attained under the stochastic
policy g.' Note that Yx and
YXg are both random variables,
just as the original variable Y.
Say we have a set of K action variables X
that occur in some temporal order.
We will indicate the time at which a given variable
is acted on by a superscript, so a variable X i occurs
before X j if i < j. For a
given X i, we denote
X< i to be the set of action
variables preceding X i.
We are interested in the probability distribution of
a set of outcome variables Y, under
a policy that sets the values of
each X i
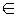 X to the output of functions
gi (known in advance) which pay attention to some
set of prior variables Zi, as well as the
previous interventions on X< i.
At the same time, the variables Zi are
themselves affected by previous interventions.
To define this recursion appropriately, we use an inductive
definition. The base case is
X1g = g1(Z1).
The inductive case is
X to the output of functions
gi (known in advance) which pay attention to some
set of prior variables Zi, as well as the
previous interventions on X< i.
At the same time, the variables Zi are
themselves affected by previous interventions.
To define this recursion appropriately, we use an inductive
definition. The base case is
X1g = g1(Z1).
The inductive case is
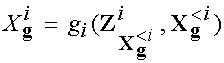 .
Here the subscript g represents the policy we use, in other
words, g = {gi | i = 1, 2, ..., K}.
We can now write the quantity of interest:
.
Here the subscript g represents the policy we use, in other
words, g = {gi | i = 1, 2, ..., K}.
We can now write the quantity of interest:
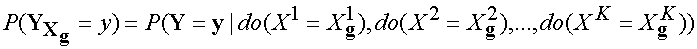
Let 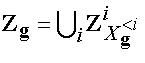 .
The key observation here is that if we observe Zg to
take on particular values, Xg collapse to unique
values as well because Xg is a function of
Zg.
We let xz = {x1z,..., xKz}
be the values attained by Xg in the situation
where Zg
has been observed to equal z = {z1,...,zK}.
We note here that if we know z, we can compute
xz in advance,
because the functions gi are fixed in advance and
known to us.
However, we don't know what values Zg might obtain, so we
use case analysis to consider all possible value combinations. We then
obtain:
.
The key observation here is that if we observe Zg to
take on particular values, Xg collapse to unique
values as well because Xg is a function of
Zg.
We let xz = {x1z,..., xKz}
be the values attained by Xg in the situation
where Zg
has been observed to equal z = {z1,...,zK}.
We note here that if we know z, we can compute
xz in advance,
because the functions gi are fixed in advance and
known to us.
However, we don't know what values Zg might obtain, so we
use case analysis to consider all possible value combinations. We then
obtain:
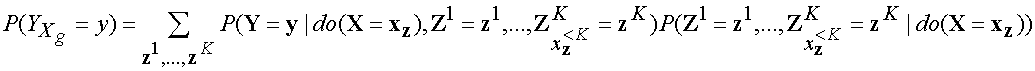
Here we note that Zi cannot depend
on subsequent interventions. So we obtain
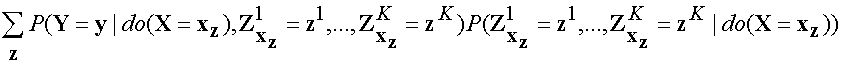
Now we note that the subscripts in the first and second terms are redundant,
since the do(xz) already implies such subscripts for
all variables in the expression. Thus we can rewrite the target quantity as
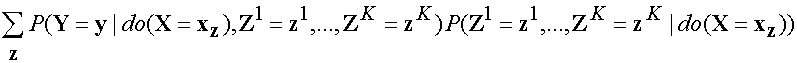
or, more succinctly,
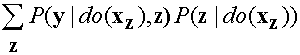
We see that we can compute this expression from
P(y | do(x)), z) and
P(z | do(x)), where Y, X, Z
are disjoint sets. Complete conditions for identifying these quantities from
a joint distribution in a given graph G are given in
[2], [1].
To summarize, though conditional plans are represented by complex nested
counterfactual expressions, their identification can nevertheless be reduced
to identification of conditional interventional distributions of the form
P(y | do(x), z) (possibly with z
being empty). Moreover, a complete condition for identifying such
distributions from evidence exists.
References
[1] Shpitser, I., and Pearl, J. Identification of conditional interventional
distributions. In Uncertainty in Artificial Intelligence (2006),
vol. 22.
[2] Shpitser, I., and Pearl, J. Identification of joint interventional
distributions in recursive semi-markovian causal models. In Twenty-First
National Conference on Artificial Intelligence (2006).
Next discussion (EPIDEM 200C: Back-door criterion
and epidemiology)
Return to Discussions
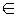 X to the output of functions
gi (known in advance) which pay attention to some
set of prior variables Zi, as well as the
previous interventions on X< i.
At the same time, the variables Zi are
themselves affected by previous interventions.
To define this recursion appropriately, we use an inductive
definition. The base case is
X1g = g1(Z1).
The inductive case is
X to the output of functions
gi (known in advance) which pay attention to some
set of prior variables Zi, as well as the
previous interventions on X< i.
At the same time, the variables Zi are
themselves affected by previous interventions.
To define this recursion appropriately, we use an inductive
definition. The base case is
X1g = g1(Z1).
The inductive case is
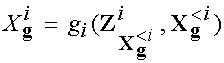 .
Here the subscript g represents the policy we use, in other
words, g = {gi | i = 1, 2, ..., K}.
We can now write the quantity of interest:
.
Here the subscript g represents the policy we use, in other
words, g = {gi | i = 1, 2, ..., K}.
We can now write the quantity of interest:
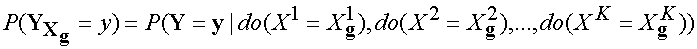
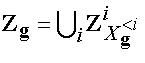 .
The key observation here is that if we observe Zg to
take on particular values, Xg collapse to unique
values as well because Xg is a function of
Zg.
We let xz = {x1z,..., xKz}
be the values attained by Xg in the situation
where Zg
has been observed to equal z = {z1,...,zK}.
We note here that if we know z, we can compute
xz in advance,
because the functions gi are fixed in advance and
known to us.
However, we don't know what values Zg might obtain, so we
use case analysis to consider all possible value combinations. We then
obtain:
.
The key observation here is that if we observe Zg to
take on particular values, Xg collapse to unique
values as well because Xg is a function of
Zg.
We let xz = {x1z,..., xKz}
be the values attained by Xg in the situation
where Zg
has been observed to equal z = {z1,...,zK}.
We note here that if we know z, we can compute
xz in advance,
because the functions gi are fixed in advance and
known to us.
However, we don't know what values Zg might obtain, so we
use case analysis to consider all possible value combinations. We then
obtain: