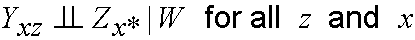CAUSALITY - Discussion (Sjolander)
Date: March 10, 2006
From: Arvid Sjolander, Dept. of Medical Epidemiology and Biostatistics, Karolinska Institutet
Subject: d-separation of counterfactuals
Question to author:
At the bottom of page 214 you mention that "any variable
that is d-separated from Z* would also be
d-separated from UZ"
(and vice versa I guess?). You conclude that
"if UZ obeys a certain independence relationship
then Zx (more generally, ZpaZ)
must obey that relationship as well" (and vice versa?). I guess that
what you mean is
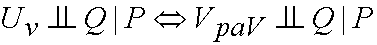
where V is any variable defined by
v = f(>paV,uV),
Q and P are any variables except V and
UV, and
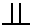 denotes independence (hope the
symbols look the same on your computer as on my).
denotes independence (hope the
symbols look the same on your computer as on my).
On the top of page 215 you use the twin network to show that
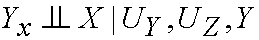
and then refer to the previous argument to state that
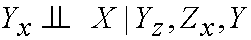
I don't see why (3) follows from (1) and (2). How can (1) justify
the replacement of UY with
Yz and UZ with
Zx in (2)? Certainly Yz is
a function of UY and Zx a
function of UZ, which
motivates one to write (2) as
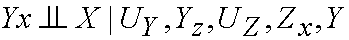
but how can you remove UY and UZ from
(4)?
If I would examine if (3) is true I would naively construct
the following triple network:
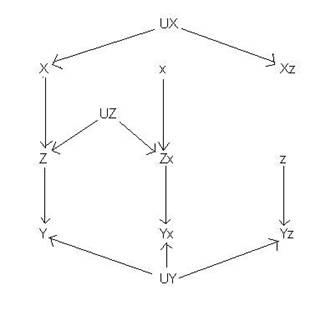
The left part corresponds to the world in which no
intervention is imposed, the middle part in which do(X=x)
is imposed, and in the right part do(Z=z) is imposed. In
this network (3) does not hold since the path
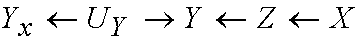 is open by conditioning on Y.
Is there anything wrong with this use of
the (generalized) twin network method?
is open by conditioning on Y.
Is there anything wrong with this use of
the (generalized) twin network method?
Author's first reply (with Ilya Shpitser)
You are, indeed, correct.
Yx is not independent of X given
Yz, Zx, Y.
However, for example, Yx is independent of X
given Zx.
Your use of d-separation in the twin network to understand
independencies between underlying counterfactual quantities is correct,
and so is your generalization of the 'twin' network to more than
two possible worlds. We called this the 'parallel worlds model' in the
path-specific effects paper.
I have spoken to Judea about (3) last spring. Our conclusion was that
(3) is not true in general, but is true if the functions from U
to their children are one to one. I believe this is the case Judea
had in mind when he wrote that section of the book.
Arvid's followup:
1) I see that a one-to-one correspondence between Uv
and VpaV is a sufficient criteria for
letting one of them serve as a proxy for the other. If
paV={}, i.e. V doesn't have any parents except
Uv, the criteria is automatically true since we
can always choose a "non-redundant coding" of Uv
such that each value V corresponds to exactly one value of
Uv. If not however, it seems to me that this criteria
implies quiet strong restrictions on the structural relationships in a
causal model. For example it completely rules out the following simple
relationship between dichotomous {z,uy} and
y=f(z,u_z):
y=1 if z=1 and uy=1
y=0 else
Is there ever a reason for assuming the criteria would hold true?
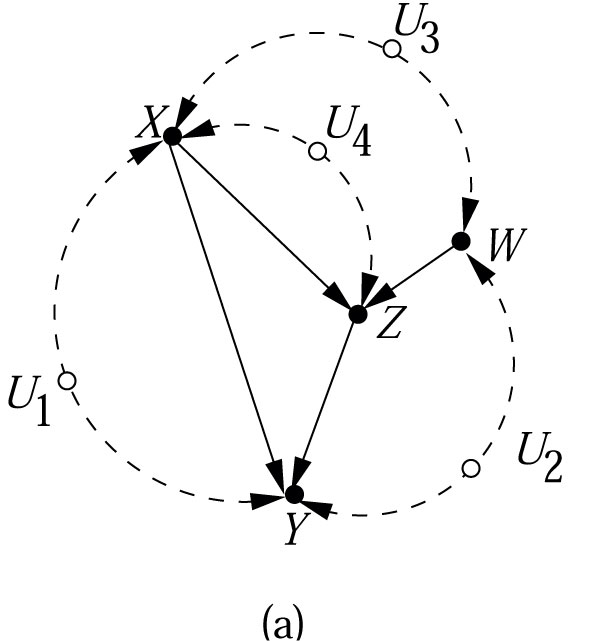
2) As a bonus your answer helped me with a similar question on the
paper "Direct and Indirect Effects" (Pearl 2001), namely "why does (7)
hold in the graph in Figure 1(a)?". If one draws a triple graph it is
obvious that the path
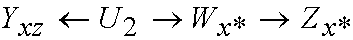 is open. If however U2 is
completely determined by W, we block the path by conditioning
on W, as in (7). But then again, do we any reason to believe
in this one-to-one correspondance in this particular setting?
is open. If however U2 is
completely determined by W, we block the path by conditioning
on W, as in (7). But then again, do we any reason to believe
in this one-to-one correspondance in this particular setting?
Reply to 1:
I think many important classes of causal models exhibit one-to-one
relationships, for example structural equation models assume all functions
are linear, and so one-to-one. Frequently we also have causal models
that contain deterministic relationships between nodes which will result
in similar changes to the way d-separation works. I agree,
though, that the original discussion in Judea's book should make clear
it's talking about the one-to-one case.
Reply to 2:
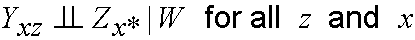
(7) actually holds in the general case in Fig 1 (a).
This is because Yxz is independent of
Zx* | Wx*.
But we know by rule 3 of do-calculus that Wx* = W.
Next discussion (Yudkowsky: The validity
of G-estimation)
Return to Discussions
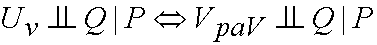
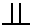 denotes independence (hope the
symbols look the same on your computer as on my).
denotes independence (hope the
symbols look the same on your computer as on my).
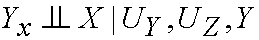
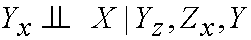
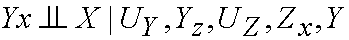

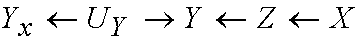 is open by conditioning on Y.
Is there anything wrong with this use of
the (generalized) twin network method?
is open by conditioning on Y.
Is there anything wrong with this use of
the (generalized) twin network method?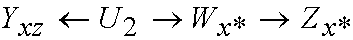 is open. If however U2 is
completely determined by W, we block the path by conditioning
on W, as in (7). But then again, do we any reason to believe
in this one-to-one correspondance in this particular setting?
is open. If however U2 is
completely determined by W, we block the path by conditioning
on W, as in (7). But then again, do we any reason to believe
in this one-to-one correspondance in this particular setting?