Many readers have asked me to comment on the relationships between problems of identification (e.g., Chapters 3-4-5) and the ultimate practical question faced by investigators: Is the conclusion we draw from the model correct? At first sight, the two seems to be unrelated; the identification problem assumes that we have a correct model, while the correctness problem questions that very assumption, that is, whether the model at hand correctly specifies the causal relationships in the world.

Professor Mulaik, for example, wrote that parameters that are identified in the erroneous model are not correctly estimated causal coefficients. "So, identification is not synonymous with correctly estimated".

Ed Rigdon wrote: "identification arises from within the model itself. Surely you do not mean to say that the "correctness" of a model also arise from within the model itself?"

An anonymous "reader from abroad" even went as far as labeling the analysis of identification in my book "wishful reasoning" and "dangerous work", writing: "Pearl supposes that the modeler is able, a priori, to determine *exactly* what the correct model is. One must be able to specify the model correctly, knowing what the possible confounding variables are, what moderators are important, etc., in advance. How reasonable is this? (amazon.com, customer review of Causality)

Author's Reply:

There is a strong correspondence between the two problems, identification and correctness, and he who shuns the former cannot fully appreciate the latter. In dealing with identification, we ask: are the model's assumptions sufficient for unique determination of a causal parameter. In dealing with correctness we ask what conditions must hold in the actual world before we can guarantee that our conclusion regarding a causal parameter is in fact correct, if tested say by experimental method. Any set of sufficient assumptions in the identification problem constitutes a set of sufficient conditions that we need to establish in the correctness problem. Thus, the correctness problem may also be viewed as the INVERSE of the identification problem, the latter asks whether a given set of conditions is sufficient, the latter asks what set of conditions would be sufficient.

To exemplify, imagine an investigator facing the following model: 

              
                                       
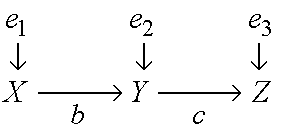
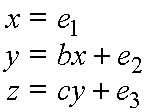
The investigator is not sure whether the model is correct, that is, not sure whether the disturbances are truly uncorrelated, or whether X indeed has no direct influence on Z. He/she asks therefore: "What should I worry about if I wish to find the true causal influence of Y on Z?"

The most informative answer the investigator can expect to obtain from the analysis of observational studies, without actually performing experiments, has the following format: "There are many conditions here for you to think about. The obvious is, of course, to ascertain that e₃ is uncorrelated with Y. (This corresponds to the classical econometric criterion of exogeneity, or "isolation" or "self-containment" that some authors perceive to be the key to correctness (Bollen, 1989, p. 44).) But even if you judge e₃ and Y to be correlated, it is still not the end of the road; other options are available. It is enough to ensure, for example, that e₂ is not correlated with e₁ and e₃. Or, if this cannot be ascertained, it is enough to ensure that e₃ is not correlated with e₁. (By "ascertaining" that e₂ and e₃ are uncorrelated I mean to exclude, on substantive grounds, the existence of significant common causes of Z and Y and, if such are found, to include them in the model).

The reason we can instruct the investigator to think about common causes of Z and X, instead of focusing on common causes of Z and Y, is that a model with cov(e₃, e₂)>0 and cov(e₃, e₁)=0 permits the identification of parameter c and, hence, if condition cov(e₃, e₁)=0 prevails, the identified estimand of c: c = R_zx/R_yx constitutes a correct estimate of the causal influence of Y on Z. We see thus how considerations of identification produce guidelines for ensuring correctness.

Clearly, to solve the correctness problems, we need techniques for quickly verifying whether a given model permits the identification of the parameter in question. It is for this reason that Causality spends several chapters on identification, and enlists powerful graphical methods for this task. Graphical techniques are also available for finding all the minimal sets of assumptions sufficient for identification (see Technical Report R-276); listing such sets constitutes a solution to the correctness problem, as it can turn into the desired advise: "Thou must ensure either: 
               1. Conditions 1, 2 and 3 , or
               2. Conditions 1, 3, 5 or, 
               3. ........ etc. etc.

Ed Rigdon was not satisfied with this explanation. He wrote: "I guess I'm just dim. If you have two variables, x and y, the regression of y on x is identified, as is the regression of x on y. But both models cannot be correct. Indeed, both may be wrong. ... it is quite possible that the correct model is not statistically identified. Thus, I don't see the value in linking identification with correctness. --Ed Rigdon

Author's Reply:

This is an illuminating comment that reflects on the interpretation of regression vs. structural parameters. It is not true that "both models cannot be correct"; both regression models ARE correct, albeit as regression models, not as causal models. Recall, regression models do not make any causal claims, and regression parameters are interpreted as conditional expectations. Thus, if we measure R_yx = 0.6, and R_xy = 0.7, all we can claim is that E(Y|x+1)- E(Y|x) = 0.6, and E(X|y+1)- E(X|y) = 0.7, and there is no reason in the world why these two claims cannot both be correct.

What Ed Rigdon probably meant to say, and rightly so, is that the following two structural models 
               M₁: y = bx + e, and
               M₂: x = cy + e',
cannot both be correct and regressional, that is, satisfying the regression condition of error uncorrelatedness: cov(y, e)=0 and cov(x, e') =0. This is indeed the case, and can be it proven within the theory of identification: the only way M₁ and M₂ can both be regressional and consistent is for c to be zero (then b is identified) or for b to be zero (then c is identified). This is the answer we expect.

Ed further wrote: "... it is quite possible that the correct model is not statistically identified. Thus, I don't see the value in linking identification with correctness."

The value of linking the two problems is demonstrated in the first example above: We started with a vague question about conditions in the world that would guarantee the correctness of a certain causal claim derived from the model, e.g., "the direct effect of Y on Z is 0.6." We then reduced it to a mathematical problem that (almost) every student can solve: "What model constraints would ensure the identification of c". (See R-276 for fuller detail of this reduction)

Finally, let us look into a case where the correct model is not statistically identified. In the second example, with y=bx+e, the correct model may have strong correlation between e and X which renders b unidentified. What happens then? We set up the correctness problem, we translate it into an identification problem, and print out the solution which reads: "For b = 0.6 to correctly represent the influence of X on Y, the omitted factors that affect Y (i.e., e) must be uncorrelated with X". This sentence sounds obvious, yet it is a "solution", and it is correct, even though there is no way for us to go and find out whether those factors (i.e., e) are indeed uncorrelated with X.

I hope no reader expects the "solution" to the correctness problem to be more than a piece of advice on what to watch for, what to include in the model and what should not be ignored. I hope no one is disappointed with us not aspiring for a more informative solution, of the form, say: "cov(e, x) is actually zero", or "yes, b = 0.6 is correct". Anyone who expects such solutions from nonexperimental data is up for a painful disappointment -- it is provenly impossible. Even those who believe, like our "reader-from-abroad, that "isolation" is prerequisite to correctness know that one cannot empirically test for isolation, and that the most one can do is to think hard about it. But, whereas "isolation" is an informal concept in want of interpretation, the identification problem provides us with concrete set of alternatives to think about.

In summary, if we wish to advise modelers what aspects of a model need careful substantive consideration to ensure the correctness of a given claim, we better prepare software providers to think about programming the inverse identification problem.

Judea
www.cs.ucla.edu/~judea