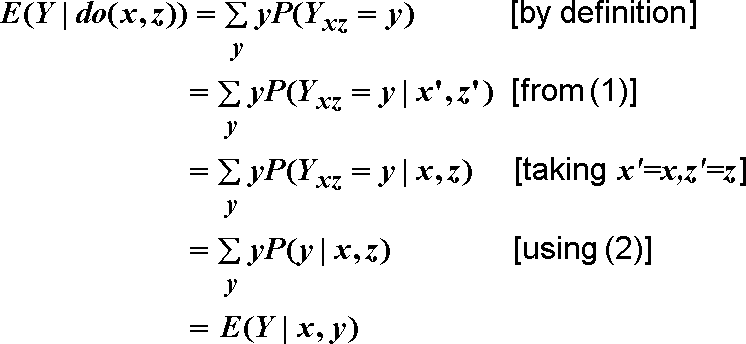New Page 2
From: Les Hayduk, University of Alberta
Date: January 1, 2001
Subject: On the Causal Interpretation of Path Coefficients
Les Hayduk asked whether the operational formula for path coefficient;
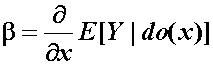 (Eq. 5.24)(Causality, page 161, Eq. (5.24))
is a calculation formula or purely an interpretation formula.
(Eq. 5.24)(Causality, page 161, Eq. (5.24))
is a calculation formula or purely an interpretation formula.
Author's reply
Like all models in science, a structural equation model (SEM) is interpreted as a mapping between physical operations
in the real world (observations, interventions, etc.) and their representative mathematical operations on the
model. The physical operation, denoted by do(x), corresponds to grabbing
variable X, setting its value at X=x, holding it at that setting and observing what happens to other variables in the world.
The mathematical operation that represents this intervention corresponds to removing the equation for
X from the model, replacing it by the equation X=x, and computing the behavior of other
variables in the newly created model. The claims made by an SEM model are encapsulated in expressions of the type
E(Y|do(x)) = 0.48 x + 0.10or
E(Y|do(x+1,z)) -
E(Y|do(x,z)) = 0.65and these correspond of course to predictions about what
we should observe in the real world if we were to execute those interventions and measure those expectations.
Thus, the operational formula for b (Causality, page 161),
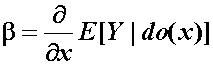 (Eq. 5.24)is both interpretational and computational. As an interpretation of b, the
formula makes predictions about empirical observations in
the world and, as a computational device, it permits the computation of b from a (fully specified) model through the
do(x) operator. In addition, it also permits the computation of b in a
partially specified model, by relating it to other model parameters, especially those that can be estimated through
experimental and nonexperimental data. This often leads to the derivation of statistical estimands
for b that are based strictly on covariances of observed variables (see below).
(Eq. 5.24)is both interpretational and computational. As an interpretation of b, the
formula makes predictions about empirical observations in
the world and, as a computational device, it permits the computation of b from a (fully specified) model through the
do(x) operator. In addition, it also permits the computation of b in a
partially specified model, by relating it to other model parameters, especially those that can be estimated through
experimental and nonexperimental data. This often leads to the derivation of statistical estimands
for b that are based strictly on covariances of observed variables (see below).
Les Hayduk further asks:
...the formula for b has no covariances on
the right hand side. Can you tell us how you think about connecting do( ) to covariances?
Author's Reply
Consider the equation y =ax +bz + e, which may be embedded in a larger SEM model.
The definition of b indeed has no covariances on the rhs; it reads:
b = E(Y|do(x,z+1)) - E(Y|do(x,z))
and the estimand of b (when b is identified) does involve covariances, as in
b = cov(Z,Y)/ var(Z)
(when e is uncorrelated with Z and X)
or
b = RYW/RYZ
(when the model contains a variable
W that is an instrument for (Z,Y))
Thus, Les' question is legitimate: How do we get the estimands from the definition?
We can do it in two ways, the first is fairly familiar to SEM researchers, the second is
more general and more instructive (demonstrated in Causality, Section 7.3.2, page 231-233).
Let us start with the first.
Once we prove that the equation: b = E(Y|do(x,z+1)) -
E(Y|do(x,z)) holds for all models, under all conditions,
(with do(x) defined as above, in terms of the equation deletion operator) we can
attend to the algebraic content of the model's equation, since the structural content of the equations is fully encapsulated
and preserved in such do-type definitions of the parameters. Taking the
model equations as algebraic relationships permits us to apply standard algebraic operations
and solve for the parameters in terms of the covariances of the variables. (Note
that not all algebraic operations are permitted on structural equations, e.g., y=ax +
e cannot be replaced by x = y/a -e/a, because this
operation destroys structural information). Algebraic solutions usually involve multiplying both sides of an equation by a
variable, taking the expectations, and solving for the target parameter. When we find a unique
solution for a parameter, say b, we say that b is identified and we associate the resulting estimand of
b with its causal interpretation. In our case, the solution would read as follows:
"The difference b = E(Y|do(x,z+1)) -E(Y|do(x,z))
can be estimated consistently by the estimand b = cov(Z,Y)
/
var(Z) if e is uncorrelated with X and Z."
Similar interpretation applies to IV-estimand or to any other estimand that one can find by algebraic methods, the only difference
would be the "if" part, namely, different modeling
assumptions should be cited, those that permit the derivation to go through. This is fairly standard in the literature,
with the exception of two ingredients; the "if" part is often left implicit, and the interpretational part is rarely
made explicit.
The second method of analysis is non-algebraic; we derive the equality
b =
E(Y|do(x,z+1)) - E(Y|do(x,z)) =
cov(Z,Y)/ var(Z)
directly from the definition of
do( ), without using the equations.
Let us demonstrate this derivation in our example. To compute the expression
E(Y|do(x,z)), we are instructed to create a new model in which
the equations for X and Z are replaced by X=x, Z=z,
and in this new model we need to compute the expectation of Y. Let us do this carefully, exactly as instructed .
Let the variable Y in the new model be denoted by Yxz.
How is the statistics of Yxz related to that of ordinary variables,
say X, Y and Z, in the original model? The relation is governed by the model assumption:
e is uncorrelated with (more generally, independent of) X and Z.
This means that variations in Yxy (which track variations in e, since
X and Z are fixed) are independent of variations in X and Z
and X and Z are constants, namely,
Yxz is independent of X and Z. More specifically,
since Yxz = ax + bz + e, we see that Yxz
is a function of e alone, not of X or Z.
Therefore, since e is independent on
any event (X=x', Z=z'), so is Yxz (for all values of
x,z,x', and z'). This permits us to write:
P(Yxz =
y|X=x', Z=z') = P(Yxz =
y) for all x' and z' (1)
In addition to (1), there is another relationship between Yzx and
X, Y and Z, that must hold, It reads:
P(Yxz =
y| X=x, Z=z) = P(Y=y|X= x,Z=z) (2)
In words, if we intervene and set the values of X and Z to the observed values
x and z, that these variables
actually took on in real life, then we have not altered the statistics of Y. (This is a general identity that
is (provenly) valid for any set of variables, regardless of the model equations. It is called consistency on page
99, eq (3.52), and it follows from the property of composition, page 229).
Using Eqs. (1) and (2), we proceed to compute the controlled
expectation E(Y|do(x,z)) as follows:
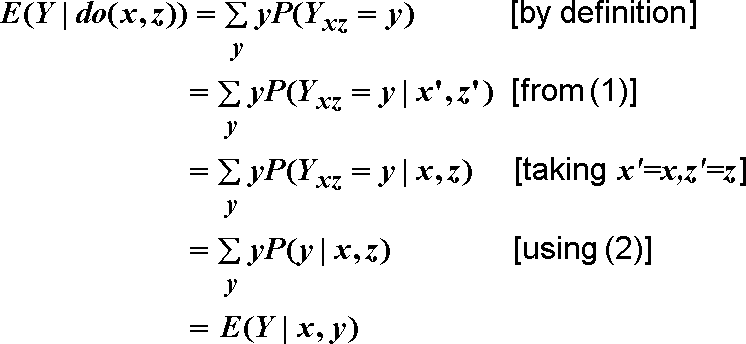
We are done, because, in linear systems, E(Y|x,y) is given by:
E(Y|x,y) =
z cov(Z,Y)/ var(Z) + x cov(X,Y)/
var(X)
From this we readily get:
b = E(Y|do(x,z+1)) -
E(Y|do(x,z)) = cov(Z,Y)/var(Z),
as expected.
This derivation is more general, because it can be applied to nonlinear
systems, and because it applies
to ANY expression involving do( ). For example, if we seek to evaluate the TOTAL
EFFECT of X on Y,
TE = E(Y|do(x+1)) -
E(Y|do(x))
this method yields the standard expression of the total effect
in terms of sums of products of path coefficients. In other words, the total effect is not
defined as sums of products of path coefficients (as in the standard literature), but rather, it is defined in terms of an independent
experiment, where one controls X and lets other variable run their natural course. The relation between the total
effect and the path coefficients are derived mathematically, from the meanings attached to total and direct effects.
Another important feature of this derivation is that it maintains clear separation between the meaning of
structural parameters and the methods used in their estimation - it lets the
meaning dictate the estimation.
Next Discussion: (Battistin:
Intuition for tight bounds under noncompliance)
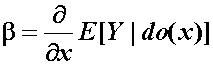 (Eq. 5.24)
(Eq. 5.24)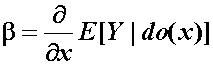 (Eq. 5.24)
(Eq. 5.24)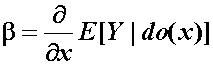 (Eq. 5.24)
(Eq. 5.24)