CAUSALITY - Discussion (Kenny)
Date: February 16, 2006
From: Dr. Patrik Hoyer (University of Helsinki, Finland)
Subject: The meaning of counterfactuals
I have a hard time understanding what counterfactuals are actually
useful for. To me, they seem to be answering the wrong question. In
your book, you give at least a couple of different reasons for when one
would need the answer to a counterfactual question, so let me tackle
these separately:
-
Legal questions of responsibility. From your text, I infer that the
American legal system says that a defendant is guilty if he or she
caused the plaintiff's misfortune. You take this to mean that if the
plaintiff had not suffered misfortune had the defendant not acted the
way he or she did, then the defendant is to be sentenced. So we have a
counterfactual question that needs to be determined to establish
responsibility. But in my mind, the law is clearly flawed.
Responsibility should rest with the predicted outcome of the
defendant's action, not with what actually happened. Let me take a
simple example: say that I am playing a simple dice-game for my team.
Two dice are to be thrown and I am to bet on either (a) two sixes are
thrown, or (b) anything else comes up. If I guess correctly, my team
wins a dollar, if I guess wrongly, my team loses a dollar. I bet (b),
but am unlucky and two sixes actually come up. My team loses a dollar.
Am I responsible for my team's failure? Surely, in the counterfactual
sense yes: had I bet differently my team would have won. But any
reasonable person on the team would thank me for betting the way I did.
In the same fashion, a doctor should not be held responsible if he
administers, for a serious disease, a drug which cures 99.99999% of the
population but kills 0.00001%, even if he was unlucky and his patient
died. If the law is based on the counterfactual notion of
responsibility then the law is seriously flawed, in my mind.
A further example is that on page 323 of your book: the desert
traveler. Surely, both Enemy-1 and Enemy-2 are equally 'guilty' for
trying to murder the traveler. Attempted murder should equal murder. In
my mind, the only rationale for giving a shorter sentence for attempted
murder is that the defendant is apparently not so good at murdering
people so it is not so important to lock him away... (?!)
-
The use of context in decision-making. On page 217, you write "At
this point, it is worth emphasizing that the problem of computing
counterfactual expectations is not an academic exercise; it represents
in fact the typical case in almost every decision-making situation." I
agree that context is important in decision making, but do not agree
that we need to answer counterfactual questions.
In decision making, the things we want to estimate is P(future |
do(action), see(context) ). This is of course a regular do-probability,
not a counterfactual query. So why do we need to compute
counterfactuals?
In your example in section 7.2.1, your query (3): "Given that the
current price is P=p0, what would be the expected value of
the demand Q
if we were to control the price at P=p1?". You argue
that this is counterfactual. But what if we introduce into the graph new
variables Qtomorrow and Ptomorrow, with parent sets
(U1, I, Ptomorrow) and (W,U)2,Qtomorrow),
respectively, and with the same connection-strengths
d1, d2, b2,
and b1. Now query (3) reads: "Given that we
observe P=p0, what would be the expected value of the
demand Qtomorrow if we perform the action
do(Ptomorrow=p1)?" This is the same
exact question but it is not counterfactual, it is just
P(Qtomorrow | do(Ptomorrow=p1),
see(P=P0)).
Obviously, we get the correct answer by doing the counterfactual
analysis, but the question per se is no longer counterfactual and can
be computed using regular do( )-machinery. I guess this
is the idea of your 'twin network' method of computing counterfactuals.
In this case, why say that we are computing a counterfactual when what
we really want is prediction (i.e. a regular do-expression)?
-
In the latter part of your book, you use counterfactuals to define
concepts such as 'the cause of X' or 'necessary and sufficient
cause of Y'. Again, I can understand that it is tempting to
mathematically define such concepts since they are in use in everyday
language, but I do not think that this is generally very helpful. Why
do we need to know 'the cause' of a particular event? Yes, we are
interested in knowing 'causes' of events in the sense that they
allows us to predict the future, but this is again a case of point
(2) above.
To put it in the most simplified form, my argument is the following:
Regardless of if we represent individuals, businesses, organizations,
or government, we are constantly faced with decisions of how to act
(and these are the only decisions we have!). What we want to know is,
what will likely happen if we act in particular ways. So we want to
know is P(future | do(action), see(context) ). We do
not want nor need the answers to counterfactuals.
Where does my reasoning go wrong?
Author reply
-
Your first question doubts the wisdom of using single-event
probabilities, rather than population probabilities in
deciding legal responsibility. Suppose there is a small
percentage of patients that are allergic to a given drug, and
the manufacturer nevertheless distributes the drug
with no warning about possible allergical reaction.
Wouldn't we agree that when an allergic patient dies
he is entitled to compensation? Normally, drug makers
take insurance for those exceptional cases, rather than
submit the entire population to expensive tests prior to
taking the drug -- it pays economically.
The physician, of course, is exonerated from guilt,
for he/she just followed accepted practice. But the
law makes sure that someone pays for the injury if
one can prove that, counterfactually, the specific death
in question would not have occured had the patient not taken the drug.
-
Your second question deals with decisions conditioned
on observations. Or, as you put it:
"In decision making, the things we want to estimate is P(future |
do(action), see(context)). This is of course a
regular do-probability, not a counterfactual query. So why
do we need to compute counterfactuals?"
The answer is that, in certain cases, the variables
entering into "context" are CONSEQUENCES of the "action",
and the expression P(y|do(x), z)
is defined as the probability of y given that we do X=x
and LATER observe Z=z, which is not the probability of y
given that we first observe Z=z and then do X=x.
This confusion disappears of course when we have a
sequential, time-indexed model. But, working with static
models as in my book, we we we do not have the language to express
the probability P of Y=y given that we first observe
Z=z and then do X=x. Counterfactuals give us a way of
expressing this probability, by writing
P = P (yx | z).
Note that P = P (yx | z) = P(y|do(x), z) if z is a non descendant of x.
I have elaborated on this point in
Pearl, J., ``The logic of counterfactuals in causal inference
(Discussion of `Causal inference without counterfactuals' by A.P. Dawid),''
Journal of American Statistical Association, Vol. 95, No. 450,
428--435, June 2000.
-
Your third question seeks a decision-theoretic
interpretation of the "actual cause" -- there is none.
The "actual cause" is defined solely by human intuition. It is
a linguistic notion often used in practical discourse, and
the task of Chapter 10 is to capture that intuition
mathematically.
Thanks for your illuminating questions. I hope that
they, together with my attempted answers will help
other readers with similar difficulties.
Best wishes,
========Judea Pearl
Date: February 22, 2006
From: Dr. Patrik Hoyer (University of Helsinki, Finland)
Subject: The meaning of counterfactuals
On Question 1
My view on your example is that if the drug company followed
the law in doing all the required tests, not "cutting corners," not
silencing early results showing strange results, not hiding
information, etc etc, then I would not consider the company responsible
for the death. Rather, I would consider it an accident, similar to the
damage cause by an earthquake, a tornado, or a car-crash due to an elk
crossing the street. Nobody would be legally responsible for the death,
but of course the family could get insurance money from a private (or
public-sector) insurance against accidental death.
Of course, had the company deliberatly tried to silence strange test
results, or not done all the tests required, or in some other way
broken the law for how medicines should be developed, then the company
(and in particular the people responsible for the practice within the
company) should be held responsible.
On question 2
My notion of causality is strongly tied to the notion of time, so I
have a hard time with your explanation.
First, isn't a "sequential, time-indexed model" really what we would
like? At least it fits nicely with my intuition about causality; much
better than any 'static' model. So, if counterfactuals are not needed
in such a model then in my mind they are not needed at all...
Second, again my intuition of causality is so strongly connected to
time that I can't understand how one can first observe Z and then do X
if Z is a descendant of X. If this is physically possible then I would
call the new controlled variablel X' and then of course Z is not a
descendant of X' (since Z happens before X') and again we can get by
with regular do-probabilities.
Author Reply On Question 2
A static model IS a short-hand notation for a
"sequential, time-indexed model".
When an engineer draws a circuit diagram, he is building a
static model, which saves miles and miles of drawing the
sequential model equivalent.
The meaning of the static model is
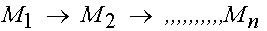
where Mi stand for the model at time ti,
and M1 = M2 = ....Mn
Now, suppose in M2 we have a chain of gates
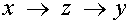 we observe Z3 at time t3 and we want
to know the causal effect of X4 on Y5 .
We can do this exercise through do-calculus, with all
the necessary indices and the replicated models.
But we can do it much nicer in the static model, using
counterfactuals.
P(Yx = y | z) will give us the correct answer.
we observe Z3 at time t3 and we want
to know the causal effect of X4 on Y5 .
We can do this exercise through do-calculus, with all
the necessary indices and the replicated models.
But we can do it much nicer in the static model, using
counterfactuals.
P(Yx = y | z) will give us the correct answer.
Isn't it a nice invention??
You say:
So, if counterfactuals are not needed
in such a model then in my mind they are not needed at all...
In principle, Multiplication is not needed in algebra -- we can live
with addition and add a number to itself as many times as needed.
But, can you honestly say that multiplication is not needed at
all? I dont think science would advanced very far without
multiplication. Same with counterfactuals.
Next discussion (Sjolander: d-separation of counterfactuals)
Return to Discussions
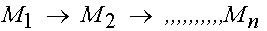
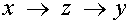 we observe Z3 at time t3 and we want
to know the causal effect of X4 on Y5 .
We can do this exercise through do-calculus, with all
the necessary indices and the replicated models.
But we can do it much nicer in the static model, using
counterfactuals.
P(Yx = y | z) will give us the correct answer.
we observe Z3 at time t3 and we want
to know the causal effect of X4 on Y5 .
We can do this exercise through do-calculus, with all
the necessary indices and the replicated models.
But we can do it much nicer in the static model, using
counterfactuals.
P(Yx = y | z) will give us the correct answer.