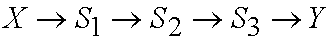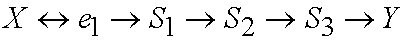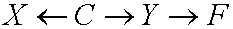Question to author
The definition of the back-door condition (Causality, page 79, Definition 3.3.1) seems to be contrived. The exclusion of descendants of X (Condition (i)) seems to be introduced as an after fact, just because we get into trouble if we dont. Why cant we get it from first principles; first define sufficiency of Z in terms of the goal of removing bias and, then, show that, to achieve this goal, you neither want nor need descendants of X in Z.

Author answer:
The exclusion of descendants from the back-door criterion is not a contrived "fix", but is based indeed on first principles. The principles are as follows: We wish to measure a certain quantity (causal effect) and, instead, we measure a dependency P(y|x) that results from all the paths in the diagram, some are spurious (the back-door paths) and some are genuine (the directed paths). Thus, we need to modify the measured dependency and make it equal to the desired quantity. To do it systematically, we condition on Z while ensuring that:

1. We block all spurious paths from X to Y,
2. We leave all directed paths unperturbed
3. We create no new spurious paths

To see why, consider the path

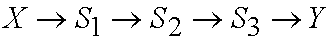
The intermediate variables, S1, S₂..., (as well as Y) are affected by noise factor e1, e2,... which are not shown explicitly in the diagram. However, under magnification, the chain unfolds into the graph:

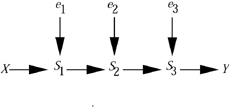
Now imagine that we condition on a descendant Z of S₁

Since S₁ is a collider, this creates dependency between X and e₁ which is equivalent to a back-door path

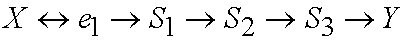
By principle 3, such spurious paths should not be created.

Note that a descendant Z of X that is not also a descendant of some S_i escapes this exclusion; it can safely be conditioned on without introducing bias. (Though it may decrease the efficiency of the associated estimator of the causal effect of X on Y.)

Further questions from Reader:
This is a reasonable explanation (for excluding descendants of X,) but it has two shortcomings:

1. It does not address cases such as
   
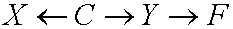
   which occur frequently in epidemiology, and where tradition permits the adjustment for Z = {C,F}
2. The explanation seems to redefine confounding and sufficiency to represent something different than what they have meant to epidemiologists in the past few decades. Can we find something in graph theory that is closest to their traditional meaning?

Author's Answer

1. The criterion given actually does cover the case you cite. The graph tells us that conditioning on Z does not introduce extra dependencies, hence, the dependency of Y on X should disappear in each stratum of Z. If we happen to measure such dependence in any stratum of Z, it must be that the model is wrong, i.e., either there is causal effect of X on Y, or some other paths exist that are not shown in the graph.

   Thus, if we wish to test the (null) hypothesis that there is no causal effect of X on Y, adjusting for Z = {C,F} is perfectly legitimate, and the graph shows it (i.e., C and F are non-descentant of X). However, it is not a legitimate adjustment for assessing the causal effect of X on Y, and the back-door criterion tells us so, because the graph under this task is
   
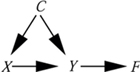
   F becomes a descendant of X, excluded by the back-door criterion.

2. The principles cited above are perfectly compatible with the definitions of confounding found in traditional epidemiology (after we clean up misguided statements made by some epidemiologists).

   If they sound at variance with traditional epidemiology, it is only because traditional epidemiologists did not have a formal system of removing and adding dependencies. All they had was healthy intuition; graphs translates this intuition into a formal system of closing and opening paths,

   We should realize that before 1985, causal analysis in epidemiology was in a state of chaos, or, as I put it politely: "a state of healthy intuition." Even the idea that confounding stands for a "difference between two dependencies, one that we want to measure, the other that we do measure" was resisted by many (see chapter 6 of Causality), because they could not express the former mathematically.

   As to finding "something in graph language that is closest to traditional meaning," we can do much better. Graphs provide the actual meaning of what we call "tradition meaning".

   In other words, graph theory is formal, traditional meaning is just intuition. Suppose we find a conflict between the two, who should we believe? tradition or formal mathematics?

   Luckily, we will never find such conflict. Why? because tradition is slippery and healthy intuition is slippery and one can always say: what they really meant was different...

   In short, what graphs gives us is the ONLY sensible interpretation of the "traditional meaning of epidemiological concepts."

Return to Discussions