CAUSALITY - Discussion (Lindley (3)) Date: September 15, 2000
From: Dennis Lindley
Subject: Reciprocal links in structural equations

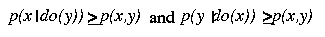
Question to author:
Equations (1.42) and (1.43) and the general issue of description by equations, still perplex me. It is incoherent to state both p(x|y) and p(y|x). (Try it with x and y binary, when these statements describe 4 values, whereas we know only 3 are needed for the joint distribution of x and y.) There are special cases, as with normal, linear regression, where the coherence is avoided. Generally I do not see how there can be two links between x and y.

Author's reply
The coherence problem you describe is precisely why we do not find any cycles in the graphical models used in statistics. We do find them in econometrics though. Graphical models in statistics are defined by conditional probability claims, while structural equations in general say nothing about p(x|y) or p(y|x). (See footnote 4, page 137). The only claims these equations make are about p(x|do(y)) and p(y|do(x)) Moreover, unlike p(x|y) and p(y|x), there are no coherence constraints on p(x|do(y)) and p(y|do(x)). The only coherence constraints we need are:

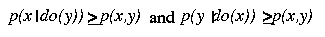
(see Eq. (9.33), page 294) and these are satisfied automatically for all parameters in Equations (1.42) and (1.43), as long as the system has a unique solution.

Next discussion (Asha: The impossibility of asymmetric causation)