Question to author:
J. Wilson from Surrey, England, asked about ways of defending his PhD thesis before examiners that do not approve of the causal interpretation of structural equation models (SEM). He complained about "the complete lack of emphasis in PhD programmes in how to defend causal interpretations and policy implications in a viva when SEM is used... if only causality had been fully explained at the beginning of the programme, then each of the 70,000 words used in my thesis would have been carefully measured to defend first the causal assumptions, then the data, and finally the interpretations.. ...( I wonder how widespread this problem is?) Back to the present and urgent task of trying to satisfy the examiners, especially those two very awkward Stats Professors - they seem to be trying to outdo each other in nastiness."

Author's reply

Dear Jonathan,
The phenomenon that you complain about is precisely what triggered my writing of Chapter 5 -- the causal interpretation of SEM is still a mystery to most SEM's researchers, leaders, educators and practitioners. I have spent hours on SEMNET Discussion List trying to deplore and rectify the current neglect, but it is only students like yourself who can turn things around and help re-instate the causal interpretation to its central role in SEM research.

As to your concrete question: How to defend the causal interpretation of SEM against nasty examiners who oppose such interpretation, permit me to assist by sketching a hypothetical scenario in which you defend the causal interpretation of your thesis in front of a hostile examiner, Dr. EX. (Any resemblance to Dr. EX is purely coincidental.)

A dialogue with a hostile examiner
or
SEM Survival Kit

For simplicity, let us assume that the model in your thesis consists of just 2-equations
y=bx + e₁
z=cy + e₂
with e₁ and e₂ possibly correlated, but neither is correlated with x. The associated diagram is given below:

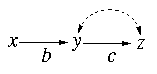
Let us further assume that the target of your thesis was to estimate parameter c, that you have estimated c satisfactorily to be c=0.78 (±0.05) using the best SEM methods, and that you have given a causal interpretation to your finding.

Now comes your nasty examiner, Dr. EX, and questions your interpretation.

EX: What do you mean by "c has a causal interpretation"?
You: I mean that a unit change in y will bring about a c units change in E(Z).

EX: The words "change" and "bring about" sound jargon to me, let's be scientific. Do you mean E(Z|y) = cy + a??? I can understand this last expression, because the conditional expectation of Z given y, E(Z|y), is well defined mathematically, and I know how to measure it. But "change" and "bring about" sound wishy washy.
You: I actually mean "change", not "conditional expectation", and by "change" I mean the following: If we have the physical means of fixing y at some constant y₁, and of changing that constant from y₁ to y₂, then the observed change in E(Z) will be c(y₂-y₁).

EX: Well Well, aren't we getting a bit metaphysical here? I never heard about "fixing" in my Statistics classes.
You: Oh, sorry, I did not realize you have statistics background. In this case, let me rephrase my interpretation a bit, to read as follows: If we have the means of conducting a controlled randomized experiment, with y randomized, then if we set the control group to y₁ and the experimental group to y₂, the observed difference in E(Z) will be E(Z₂)-E(Z₁) = c(y₂-y₁) regardless of what values y₁ and y₂ we choose. (Z₁ and Z₂ are the measurements of z under the control and experimental groups, respectively)

(Footnote: Just in case EX asks: "Is that the only claim?" you should add: Moreover, I claim that the entire distribution of the random variable Z₁-cy₁ will be the same as that of the variable Z₂-cy₂.)

EX: That sounds much closer to what I can understand. But I am bothered by a giant leap that you seem to be making. Your data was nonexperimental, and in your entire study you have not conducted a single experiment. Are you telling us that your SEM exercise can take data from observational study, do some hocus focus LISREL analysis on it, and come up with a prediction of what the outcome of a controlled randomized experiment will be? You got to be kidding!! You know how much money can be saved nationwide if we could replace experimental studies with SEM magic?
You: This is not magic, Dr. EX, it is plain logic. The input to my LISREL analysis was more than just nonexperimental data. The input consisted of two components: (1) data, (2) causal assumptions; my conclusion logically follows from the two. The second component is absent in standard experimental studies, and that is what makes them so expensive.

EX: What kind of assumptions? "causal"? I never heard of such strangers, and, looking at your model, I do not see anything strange there but equations.
You: These are not ordinary algebraic equations Dr. EX. These are "structural equations", and if we read them correctly, they convey a set of assumptions with which you are familiar, namely, assumptions about the outcomes of hypothetical randomized experiments conducted on the population -- we call them "causal" or "modeling" assumptions, for want of better words, but they are merely assumptions about the behavior of the population under various randomized experiments.

EX: Wait a minute! Now that I begin to understand what your causal assumptions are, I am even more puzzled than before. If you allow yourself to make assumptions about the behavior of the population under randomized experiments, why conduct any study? Why not make the assumption directly that in a randomized experiment, with y randomized, the observed difference in E(Z) should be c'(y₂-y₁), with c' just any convenient number, and save yourself agonizing months of data collection and analysis . He who believes your other untested assumptions should also believe your E(Z₂)-E(Z₁) = c'(y₂-y₁) assumption.
You: Not so, Dr. EX. The modeling assumptions with which my program begins are much milder than the assertion E(Z₂)-E(Z₁) = 0.78(y₂-y₁) with which my study concludes. First, my modeling assumptions are qualitative, while my conclusion is quantitative, making a commitment to a specific value of c, c=0.78. Second, many researchers (including you, Dr. EX) would be prepared to accept my assumptions, not my conclusion, because the former conforms to commonsense understanding and general theoretical knowledge of how the world operates. Thirdly, the majority of my assumptions can be tested by experiments that do not involve randomization of y. This means that if randomization y is expensive, or infeasible, we still can test the assumptions by controlling other, less formidable variables. Finally, though this is not the case in my study, modeling assumptions often have some statistical implications that can be tested in nonexperimental studies, and, if the test turns successful (we call it "fit"), it gives us further confirmation of the validity of those assumptions.

EX: This is getting interesting. Let me see some of those "causal" or modeling assumptions, so I can judge how mild they are.
You: That's easy, have a look at our model

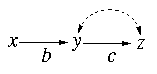
where z - student's score on the final exam
          y - number of hours the student spent on homework
          x - weight of homework (as announced by the teacher) in the final grade.

When I put this model down on paper, I had in mind two randomized experiments, one where x is randomized (i.e., teachers assigning weight at random), the second where the actual time spent on homework (y) is randomized. The assumptions I made while thinking of those experiments were:

1. Linearity and exclusion for y: E(Y₂)-E(Y₁)= b(x₂-x₁), with b unknown (Y₂ and Y₁ are the times that would be spent on homework under announced weights x₂ and x₁, respectively.) Also, by excluding z from the equation, I assumed that the score z would not affect y, because z is not known at the time y is decided.
2. Linearity and exclusion for z: E(Z₂)-E(Z₁)=c(y₂-y₁) for all x, with c unknown. In words, x has no effect on z, except through y.

   In addition, I made assumptions about the factors that govern x under nonexperimental conditions.

3. Exogeneity of x: I assumed that, under nonexperimental conditions, there are no common causes for x and y or of x and z.

EX: HM, HM, Well, I agree that these assumptions are milder than a blunt, unsupported declaration of your thesis conclusion E(Z₂) - E(Z₁) = 0.78 (y₂-y₁), and I am somewhat amazed that such mild assumptions can support a daring prediction about the actual effect of homework on score (under experimental setup). But I am still unhappy with your exogeneity assumption. It seems to me that a teacher who emphasizes the importance of homework would also be an inspiring effective teacher so, e₂ (which includes factors such as quality of teaching) should be correlated with x, contrary to your assumption.

You: Dr. EX, now you begin to talk like an SEM researcher. Instead of attacking the method and its philosophy, we are begining to discuss substantive issues -- e.g., whether it is reasonable to assume that teacher's effectiveness is uncorrelated with the weight that teacher assigns to homework. I personally have had great teachers that could not care less about homework, and conversely so.

But this is not what my thesis is all about. I am not claiming that teacher's effectiveness is uncorrelated with how they weigh homework, I leave that to other researchers to test in future studies (or it might have been tested already?) All I am claiming is: Those researchers who are willing to accept the assumption that teachers' effectiveness is uncorrelated with how they weigh homework, will find it interesting to note that this assumption, coupled with the data, logically implies the conclusion that an increase of one homework-hour per day causes an (average) increase of 0.78 grade points in student's score. And this claim can be verified empirically if we are allowed a controlled experiment with randomized amounts of homework (y).

EX: I am glad you do not insist that your modeling assumptions are true; you merely state their plausibility and explicate their ramifications. I cannot object to that. But I have another question. You said that your model does not have any statistical implications so it cannot be tested for fit to data. How do you know that? and doesn't this bother you?
You: I know it by just looking at the graph and examining the missing links. A criterion named d-separation (see discussion under "d-separation without tears") permits students of SEM to glance at a graph and determine whether the corresponding model implies any constraint in the form of a vanishing partial correlation between variables. Most statistical implications (though not all) are of this nature. The model in our example does not imply any constraint on the covariance matrix, so it can fit perfectly any data whatsoever. We call this model "saturated", a feature that some SEM researchers, unable to shake off statistical-testing traditions regard as an awful, basic fault of the model. It isn't. Having a saturated model at hand simply means that the investigator is not willing to make bold causal assumptions, and that the mild assumptions he/she is willing to make are too weak to produce statistical implications. Such conservative attitude should be commended, not condemned. Admittedly, I would be happy if my model were not saturated, say if e₁ and e₂ were uncorrelated. But this is not the case at hand; commonsense tells us that e₁ and e₂ are correlated and it also shows in the data. I tried assuming cov(e₁,e₂)=0, and I got terrible fit. Am I going to make unwarranted assumptions just to get my model Knighted as "non-saturated"? No! I would rather make reasonable assumptions, get useful conclusions, and report my results side by side with my assumptions.

EX: But suppose there is another saturated model, based on equally plausible assumptions, yet leading to a different value of c. Shouldn't you be concerned with the possibility that some of your initial assumptions are wrong, hence that your conclusion c=0.78 is wrong? And there is nothing in that data that can help you prefer one model over the other.

You: I am concerned indeed and, in fact, I can immediately enumerate the structures of all such competing models. For example:
     .
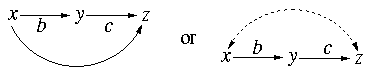
and many more. (This, too, can be done using the d-separation criterion, see Causality, pp. 145-8.) But note that the existence of competing models does not in any way weaken my earlier stated claim: "Researchers who accept the qualitative assumptions of model M are compelled to accept the conclusion c = 0.78." This claim remains logically invincible. Moreover, the claim can be further refined by reporting the conclusions of each contending model, together with the assumptions underlying that model. The format of the conclusion will then read:

If you accept assumption set A₁, then c=c₁ is implied,
If you accept assumption set A₂, then c=c₂ is implied,
and so on...

EX: I see, but still, in case we wish to go beyond these conditional statements and do something about deciding among the various assumption sets, are there no SEM methods to assist one in this endeavor? We, in statistics, are not used to be facing problems with two competing hypotheses that cannot be submitted to some test, however feeble.
You: This is a fundamental difference between statistical data analysis and SEM. Statistical hypotheses, by definition, are testable by statistical methods. SEM models, in contrast, rest on causal assumptions which, also by definition (see Causality, p. 39), cannot be given statistical tests. If our two competing models are saturated, we know in advance that there is nothing more we can do but to report our conclusions in a conditional format, as listed above. If, however, the competition is among equally plausible yet statistically distinct models, then we are facing the century-old problem of model selection, where various selection criteria such as AIC have been suggested for analysis. However, the problem of model selection is now given a new, causal twist -- our mission is not to maximize fitness, nor to maximize predictive power, but rather, to produce the most reliable estimate of causal parameters such as c. This is a new arena altogether (See R-276).

EX: Interesting. One last question. You started talking about randomized experiments only after realizing that I am a statisticians. How would you explain your SEM strategy to a non-statistician?
You: I would use plain English and say: "If we have the physical means of fixing y at some constant y₁, and of changing the constant from y₁ to y₂, then the observed change in E(Z) would be c(y₂-y₁)." Most people understand what "fixing" means, because this is on the mind of policy makers. For example, a teacher interested in the effect of homework on performance does not think in terms of randomizing homework. Randomization is merely an indirect means for predicting the effect of fixing.

Actually, if the person I am talking to is really enlightened (and many statisticians are), I might even resort to counterfactual conversation and say, for example, that a student who scored z on the exam after spending y hours on homework would have scored z + c had he/she spent y+1 hours on homework. To be honest, this is what I truly had in mind while writing the equation z = cy + e₂, where e₂ stood for all other characteristics of the student that were not given variable names in our model and that are not affected by y. I did not even think about E(Z), only about z of a typical student. Counterfactuals are the most precise linguistic tool we have for expressing the scientific meaning of functional relations. But I refrain from mentioning counterfactuals when I talk to statisticians because, and this is regrettable, statisticians tend to suspect deterministic concepts that are not immediately testable, and counterfactuals are such concepts (see JASA, June 2000, for discussion of causality without counterfactuals)

EX: Thanks for educating me on these aspects of SEM. No further questions.
You: The pleasure is mine.

Next Discussion (L.B.S. / S.M.: Can do(x) represent practical experiments?)