Question to author:
The parameter identification method described in Section 5.3.1 rests on two criteria: (1) The single door criterion of Theorem 5.3.1, and the back-door criterion of Theorem 5.3.2. This method may require appreciable bookkeeping in combining results from various segments of the graph. Is there a single graphical criterion of identification that unifies the two Theorems and thus avoids much of the bookkeeping involved?

Author's reply
This is a very insightful question, thanks!. The answer is: Yes. The unifying criterion is described in the following Lemma.

Lemma 1 (Graphical identification of direct effects)
Let c stand for the path coefficient assigned to the arrow X --> Y in a causal graph G. Parameter c is identified if there exists a pair (W, Z), where W is a single node in G (not excluding W=X), and Z is a (possibly empty) set of nodes in G, such that:

1. Z consists of nondescendants of Y,
2. Z d-separates W from Y in the graph G_c formed by removing X --> Y from G.
3. W and X are d-connected, given Z, in G_c.

Moreover, the estimand induced by the pair (W, Z) is given by:

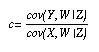
The idea of unifying the two criteria came to me while reading Rod McDonald's recent paper "What can we learn from the path equations?" (Submitted). I have used this Lemma in a new report (R-276.pdf) / (R-276.ps), "Parameter identification: a new perspective". This report removes major inconsistencies in traditional definitions of parameter overidentification and offers graphical methods for deciding the degree to which a parameter is overidentified in a given model.

Next discussin (Hagenaars: Indirect effects in nonlinear models)