d-SEPARATION WITHOUT TEARS
(At the request of many readers)
Introduction
d-separation is a criterion for deciding, from a given a causal graph, whether a set X of variables is independent of another set Y, given a third set Z. The idea is to associate "dependence" with "connectedness" (i.e., the existence of a connecting path) and "independence" with "unconnected-ness" or "separation". The only twist on this simple idea is to define what we mean by "connecting path", given that we are dealing with a system of directed arrows in which some vertices (those residing in Z) correspond to measured variables, whose values are known precisely. To account for the orientations of the arrows we use the terms "d-separated" and "d-connected" (d connotes "directional").We start by considering separation between two singleton variables, x and y; the extension to sets of variables is straightforward (i.e., two sets are separated if and only if each element in one set is separated from every element in the other).
1. Unconditional separation
Rule 1: x and y are d-connected if there is an unblocked path between them.
By a "path" we mean any consecutive sequence of edges, disregarding their directionalities. By "unblocked path" we mean a path that can be traced without traversing a pair of arrows that collide "head-to-head". In other words, arrows that meet head-to-head do not constitute a connection for the purpose of passing information, such a meeting will be called a "collider".
Example 1
![]()
This graph contains one collider, at t.
The path x-r-s-t is unblocked, hence x and t are
d-connected. So is also the path t-u-v-y, hence
t and y are d-connected, as well as the pairs
u and y, t and v, t and u, x and s etc....
However, x and y are not d-connected; there is no
way of tracing a path from x to y without traversing
the collider at t.
Therefore, we conclude that x and y are d-separated,
as well as x and v, s and u, r and u, etc.
(The ramification is that the covariance terms corresponding
to these pairs of variables will be zero, for every choice
of model parameters).
1.2 blocking by conditioning
Motivation: When we measure a set Z of variables, and take their values as given, the conditional distribution of the remaining variables changes character; some dependent variables become independent, and some independent variables become dependent. To represent this dynamics in the graph, we need the notion of "conditional d-connectedness" or, more concretely, "d-connectedness, conditioned on a set Z of measurements".
Rule 2: x and y are d-connected, conditioned on a set Z of nodes, if there is a collider-free path between x and y that traverses no member of Z. If no such path exists, we say that x and y are d-separated by Z, We also say then that every path between x and y is "blocked" by Z.
Example 2
![]()
Let Z be the set {r, v} (marked by circles in the figure). Rule 2 tells us that x and y are d-separated by Z, and so are also x and s, u and y, s and u etc. The path x-r-s is blocked by Z, and so are also the paths u-v-y and s-t-u. The only pairs of unmeasured nodes that remain d-connected in this example, conditioned on Z, are s and t and u and t. Note that, although t is not in Z, the path s-t-u is nevertheless blocked by Z, since t is a collider, and is blocked by Rule 1.
1.3. Conditioning on colliders
Motivation: When we measure a common effect of two independent causes, the causes becomes dependent, because finding the truth of one makes the other less likely (or "explained away"), and refuting one implies the truth of the other. This phenomenon (known as Berkson paradox, or "explaining away") requires a slightly special treatment when we condition on colliders (representing common effects) or their descendants (representing effects of common effects).
Rule 3: If a collider is a member of the conditioning set Z, or has a descendant in Z, then it no longer blocks any path that traces this collider.
Example 3
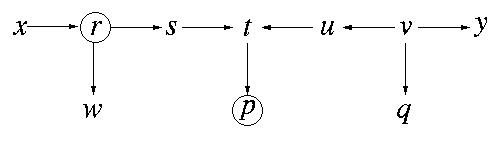
Let Z be the set {r, p} (again, marked with circles). Rule 3 tells us that s and y are d-connected by Z, because the collider at t has a descendant (p) in Z, which unblocks the path s-t-u-v-y. However, x and u are still d-separated by Z, because although the linkage at t is unblocked, the one at r is blocked by Rule 2 (since r is in Z).
This completes the definition of d-separation, and the reader is invited to try it on some more intricate graphs, such as those shown in Figure 1.3
Typical application:
Suppose we consider the regression of y on p, r and x,
Remark on correlated errors:
Correlated exogenous variables (or error terms)
need no special treatment. These are represented
by bi-directed arcs (double-arrowed) and their arrowheads are treated
as any other arrowhead for the purpose of path tracing.
For example, if we add to the graph above a bi-directed arc
between x and t, then y and x will no longer
be d-separated (by Z={r, p}), because the path
x-t-u-v-y is d-connected --- the collider at t is
unblocked by virtue of having a descendant, p, in Z.